GEARS
- Aminur _
- Nov 18, 2022
- 3 min read
Updated: Nov 19, 2022
WHAT'S UP FAMALAM? WELCOME BACK TO BLOG ENORMOUS. In Today's blog, I'll be
sharing my wonderful experience playing with gears in one of my practicals.
Surprisingly, this isn't my first time playing with gears. When I was in Primary School, my parents would buy me contraptions which I could put together and gears were a key factor in most of my builds. Okay, enough about the past, I'll now share the theoretical and practical knowledge I gained from the practical session itself.
1. The definition of gear module, pitch circular diameter and the relationship between gear module, pitch circular diameter and number of teeth.
Gear Module
"Module" is the unit of size that indicates how big or small a gear is. It is the ratio of the reference diameter of the gear divided by the number of teeth. This basically means that the gear module refers to the size of each individual tooth on a gear.

Pitch Circulation Diameter
The Pitch Circle Diameter (PCD) is the diameter of the circle
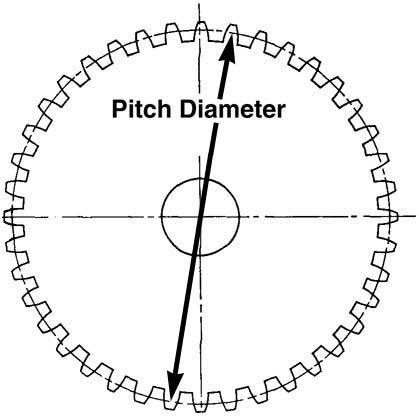
which passes through the centre of all the studs, wheel bolts or wheel rim holes.
Relationship between Gear Module, PCD & number of teeth.
Gear Module = PCD/number of teeth
2. Relationship between gear ratio (speed ratio) and output speed, between gear ratio and torque for a pair of gears.
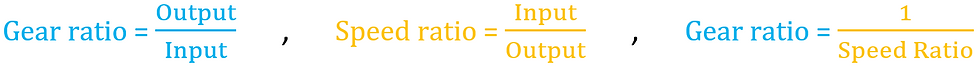
Relationship between gear ratio (speed ratio) and output speed for a pair of gears.

From the set of equations above; when a pair of gears has a low gear ratio, the output speed for the pair of gears will be high and vice versa. Therefore, the gear ratio is inversely proportional to the output speed.
Relationship between gear ratio and torque for a pair of gears.
Torque is the measure of the force that can cause an object to rotate about an axis.

The equation above shows that output torque for a pair of gears would be high when the gear ratio is high. Therefore, the gear ratio is directly proportional to torque.
3. Proposed design to make the hand-squeezed fan better:
Initial Design of the hand-squeezed fan

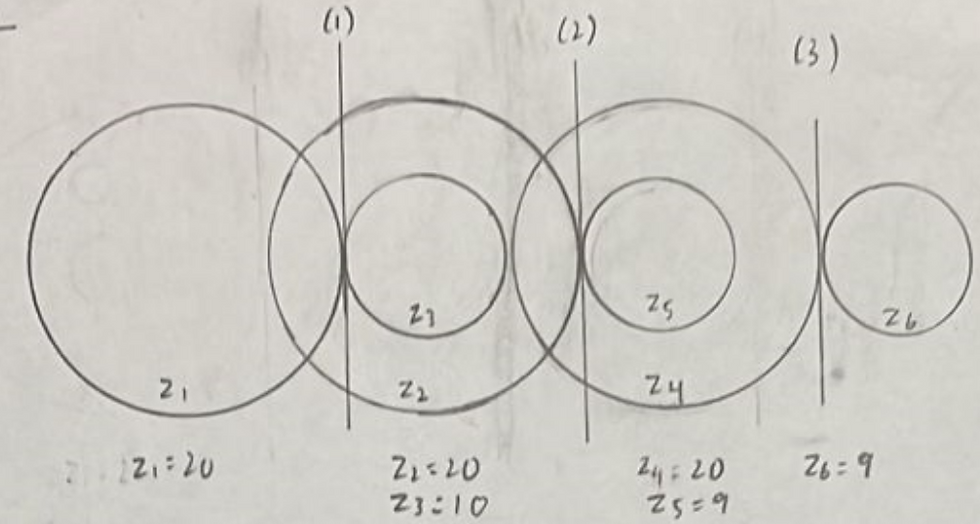

For every time the handle was cranked, the turbine spun 10 rounds
Proposed design to make it better
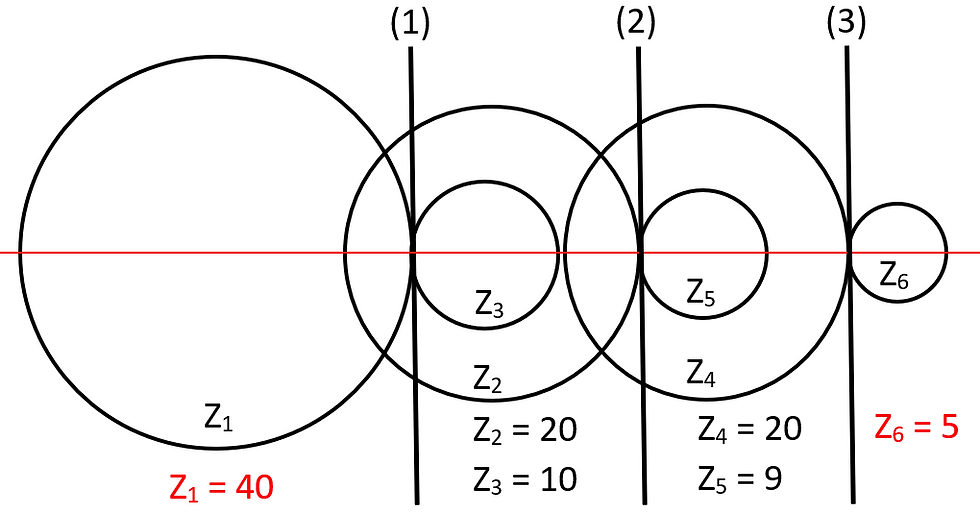
Increase the size of the input gear, Z1.
Decrease the size of the output gear, Z6.
By doing so, we can increase the speed ratio of the overall system.
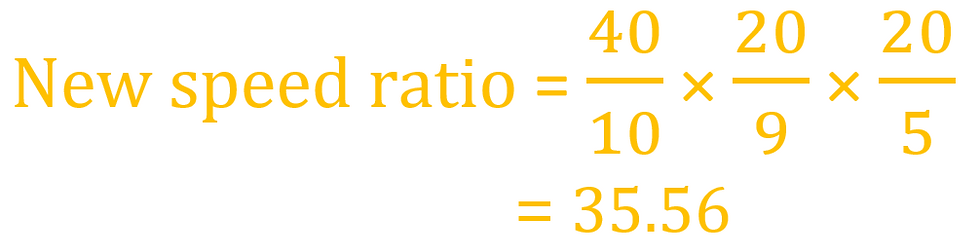
With the new and improved design, the new speed ratio is 3.6x the initial speed ratio.
For every time the handle is cranked, the turbine will spin 36 times.
4. Descriptions on how my practical team arranged the gears provided in the practical to raise the water bottle.
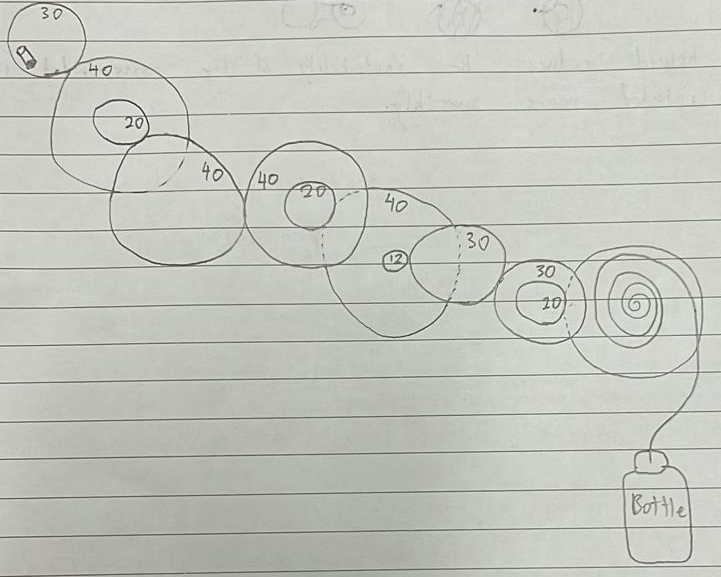
a. Calculation of the gear ratio (speed ratio)
Since we are an ambitious team, we tried our best to attain the highest gear ratio possible via a compound gear train to assert our dominance.
b. Photo of the actual gear layout.

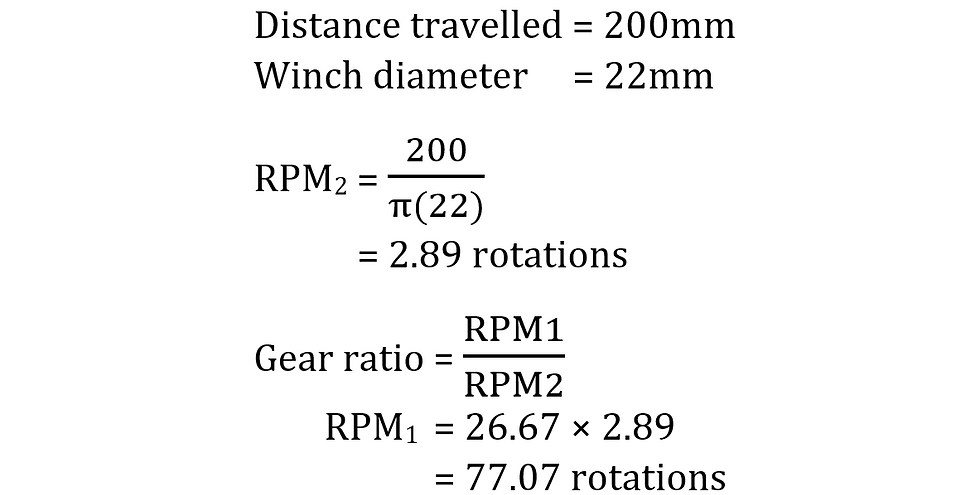
c. Calculation of the number of revolutions required to rotate the crank handle.
d. The video of the turning of the gears to lift the water bottle.
5. Below is my Learning Reflection on the gears activities
This practical felt very refreshing to me as it has been a long time since I worked with my classmates for a hands-on practical involving mechanics. Before the practical itself, my friends and I stayed up late the day before to watch the 4 videos regarding gears together. The main takeaway from these videos was how to calculate the gear ratio for a simple gear train and for a compound gear train.
During the practical itself, we were all very anxious about our groupings as we'd be working with them for all other practicals for the rest of the semester. Fortunately, I was teamed up with Devin, Jun Kai, Ji Hinn, and Jia Tong, a pretty overpowered team if I do say so myself. We mainly had 3 tasks to complete so we distributed the work equally amongst ourselves to not be behind on time. Ji Hinn volunteered to complete the worksheet, Devin and Jia Tong worked on the hand-powered fan, whilst Jun Kai and I played around with gears to raise a 500mL water bottle up 20cm.
Activity 1: Lifting water using gears
One of the advantages Jun Kai and I had when working on our part is that we are very hands-on engineers. We understood that we had to use all the gears provided to us and that the gear ratio should at least be greater than 1. So we applied the concept of the compound gear train to our planning and we eventually created a gear train with a gear ratio of 26.67. By having such a high gear ratio, we were able to move our handle very easily, however, it required almost 88 revolutions to fully raise the water up by 20cm. This got me thinking about the law of conservation of energy and how it also applies in these scenarios. In our case, we required very little strength to turn the handle but a lot of revolutions was required, compared to the other groups with a lower gear ratio, they required a substantial amount of strength to turn their handle but only required less than 10 revolutions to raise their water bottle.
Along the way, Jun Kai and I learnt a few valuable lessons regarding the efficiency of gears.
It's very important that the gears are tightly connected to one another to prevent them from skidding over each other.
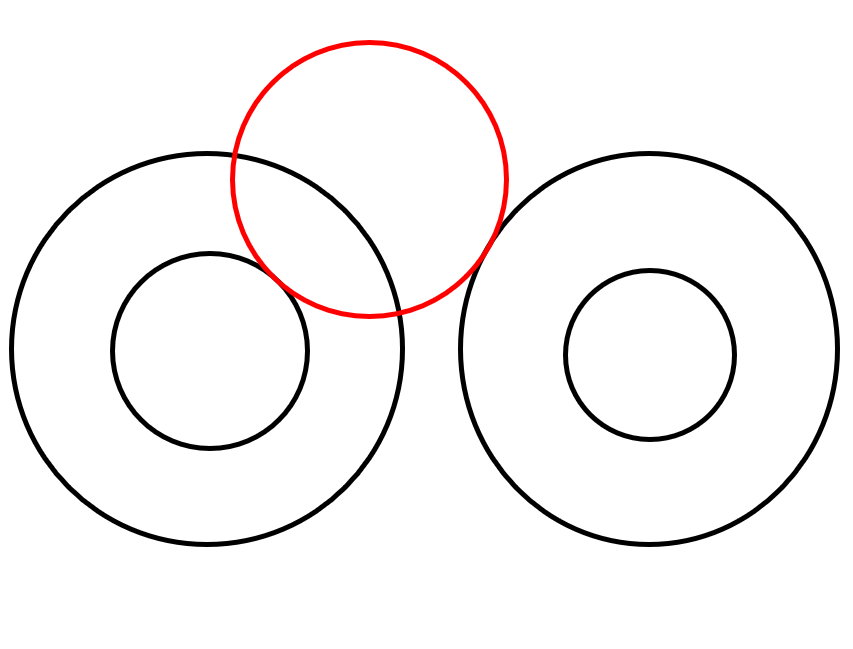
In some scenarios when a gear is suspended (not touching the backboard) in between two other gears, It's important to ensure that the suspended gear is above the other two other gears as shown in the image to the right. This helped one of our suspended gears in our design from shaking as often compared an another suspended gear below two other gears.
Friction is always going to be present in between a pair of gears. Thus the actual number of revolutions required will always be more than the theoretical number of revolutions calculated.
Activity 2: Hand-powered fan
This activity cause a lot of headaches for Devin and Jia Tong becasue they were trying the figure out why their fan wasn't moving. After seeking for assistance from our Technical Executive, Ms Serene, she recommended that we use another set from another group. It turned out that our initial set was faulty becuase the second set worked perfectly fine Another challenge we faced was actually counting the number of fan rotation per crank. We tried filming multiple slow motion videos but the fan was moving way to fast. So once again, with the help of Ms Serene and her unbeatable practical skills, we finally concluded that for every handle cranked, the fan would ratate 10 times.
Overall, I had an amazing time playing with gears again and I', extremely proud of my team for what we managed to accomplish. From this practical, I think I have a rough idea on how I can implement gears into my CA2 project about a Carbon Monoxide Ventilation System.



Comments